重新开坑coq兼复盘之前的三个未解之谜
其实在挺久以前有试过啃 coq 来着,虽然后来就放弃了(大概停留在 Logic 和 Tactics 两章之间)。
这次重新开坑倒是还算顺利,可能因为这之后在fp方面有了一些积累,对于命题的归纳证明也有了更直观的认知。借着万圣节放假的时候半个星期左右啃到了 Logic 一章。
当然这里面也有一部分原因是因为有参考到之前的题解,well,not
really,一方面因为有许多题目自己直接 intros induction destruct
开场基本上就能搞定,
也就不是很需要看之前的题解,另外一方面这次也更仔细地读了那本书,也意识到之前有许多题目的解法是错误的(所以解不出),而且即使能解出来也不是最佳的做法就是了。
上一次啃 coq 的时候卡住的最后几题有截图保留下来,现在回过头看解法也都很显然了。这次先把这几道题的解题思路写下来当备忘好了。之后也会整理一下其他用到的或者讲到的 tactics 的用法和一些值得关注的地方(如果有精力的话)。
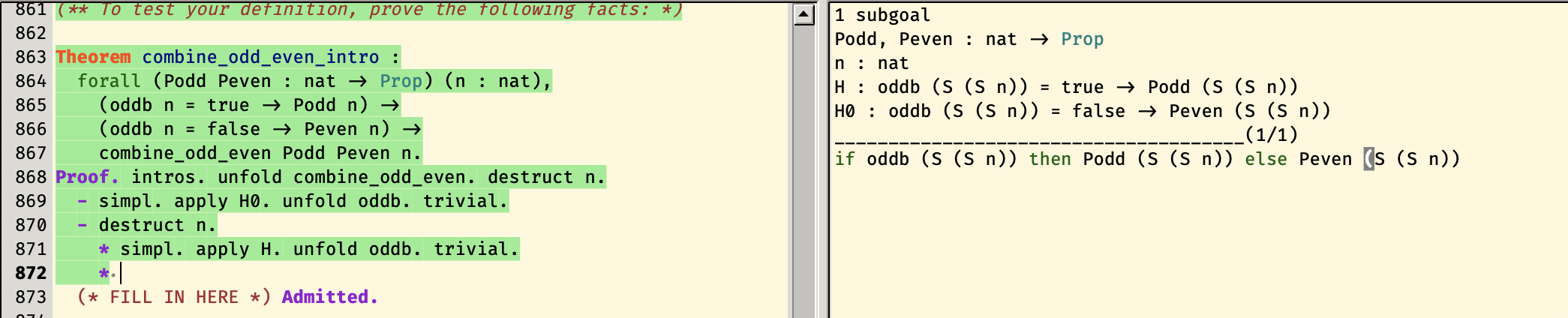
这里的正确的解法是destruct (odd n)而不是destruct n,这样的话,会产生两个分支,分别是把odd
n变成true和false,代入到??? = true -> Podd n
和??? = false -> Peven n,而subgoal本身也从if odd n then Podd n else Peven n变成分别是Podd n和Peven n两个subgoal。接下来只要
apply就完事了(
需要留意到的点其实就两个,一个是bool本身是 inductive
的,对它做destruct会得到true以及false,另一个就是,destruct本身可以去拆一个
表达式,例如(odd n),而不仅仅是一个变量。
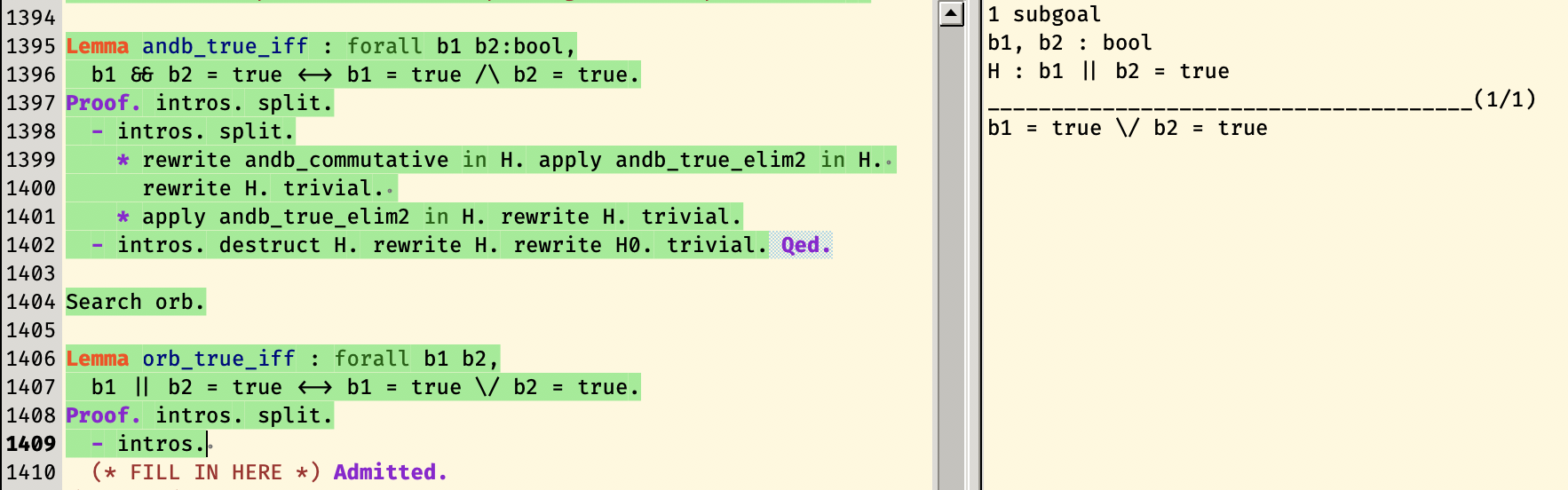
这里的解法也很明显,对 b1 然后是 b2
做induction,再分别讨论不同的
subgoal,如果在假设里面出现了true = false这样的明显不可能成立的场合,用
discriminate或者inversion即可。
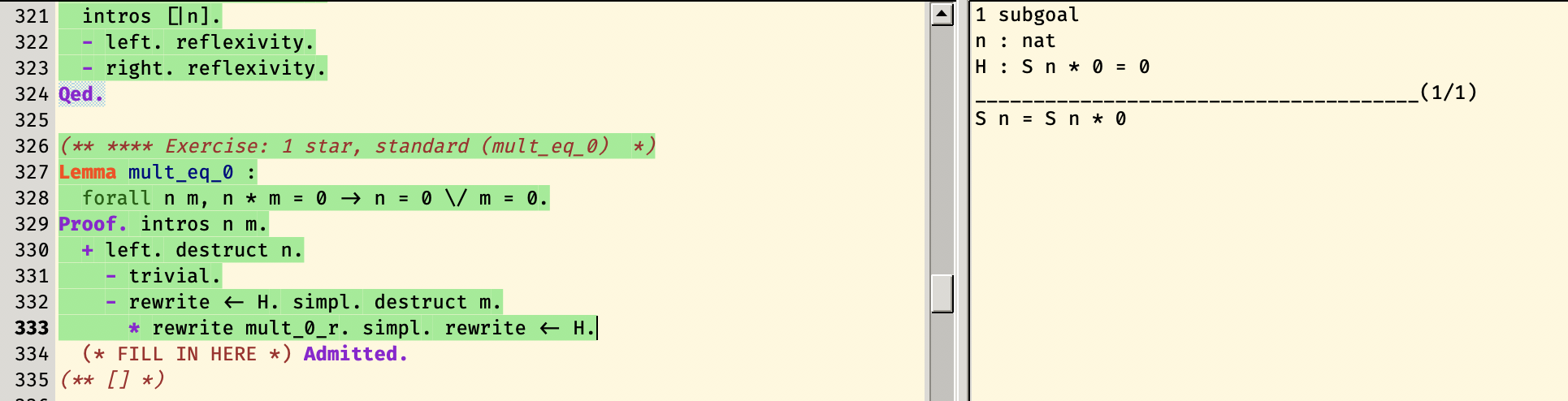
在SF里面这个 Lemma
改名了,实际上对应的是mult_is_O。就mult_eq_0而言,只要apply前面的两个小引理就可以了。至于mult_is_O,也就是这里的
这个
Lemma,问题在于过早left,也就是在n = 0 \/ m = 0里面选择了n = 0,也就是「假设n = 0必定成立」。然而在这里根据假设,n和m都有可能为0。
去掉了m = 0的可能性后,对于S n = 0的情况,化简后可得S n = S n * 0,显然,这是不可能成立的。
解决办法是先destruct n(m其实也可以),把析取的结构保留在
subgoal 里,然后再对 nat
做destruct,当n = 0的时候可得0 = 0,直接trivial。
对于S n,有S n * m = 0做前提,subgoal
S n = 0 \/ m = 0的左边不去管它,这里有两种策略:
直接取right,因为已知
S n = 0不可能成立,然后再destruct m,首先得到0 = 0这样的情况,trivial,然后是S m = 0,在前提为S n * S m = 0(显然为假)的情况下,discriminate H(inversion也行)。先
destruct m,得到两个析取式,对于第一个,因为右边有0 = 0的情况,直接right. trivial.,接下来的 subgoal 为S n = 0 \/ S m = 0同时 前提为S n * S m = 0,也是只要discriminate H即可。
inversion本身是个比较难懂的
tactic,其实到现在也没太明白这个 tactic 具体是做什么的。
回过头看的话,其实都是很基础的操作了(bushi
大概就是这样了。